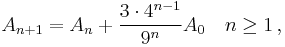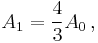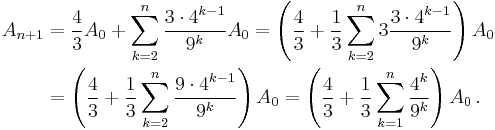Koch snowflake
The Koch snowflake (also known as the Koch star and Koch island[1]) is a mathematical curve and one of the earliest fractal curves to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: "Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire") by the Swedish mathematician Helge von Koch.
Contents |
Construction
The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows:
- divide the line segment into three segments of equal length.
- draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.
- remove the line segment that is the base of the triangle from step 2.
After one iteration of this process, the resulting shape is the outline of a hexagram.
The Koch snowflake is the limit approached as the above steps are followed over and over again. The Koch curve originally described by Koch is constructed with only one of the three sides of the original triangle. In other words, three Koch curves make a Koch snowflake.
Properties
The Koch curve has an infinite length because each time the steps above are performed on each line segment of the figure there are four times as many line segments, the length of each being one-third the length of the segments in the previous stage. Hence, the total length increases by one third and thus the length at step n will be (4/3)n of the original triangle perimeter: the fractal dimension is log 4/log 3 ≈ 1.26, greater than the dimension of a line (1) but less than Peano's space-filling curve (2).
The Koch curve is continuous everywhere but differentiable nowhere.
Taking s as the side length, the original triangle area is 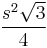 . The side length of each successive small triangle is 1/3 of those in the previous iteration; because the area of the added triangles is proportional to the square of its side length, the area of each triangle added in the nth step is 1/9 of that in the (n-1)th step. In each iteration after the first, 4 times as many triangles are added as in the previous iteration; because the first iteration adds 3 triangles then the nth iteration will add
. The side length of each successive small triangle is 1/3 of those in the previous iteration; because the area of the added triangles is proportional to the square of its side length, the area of each triangle added in the nth step is 1/9 of that in the (n-1)th step. In each iteration after the first, 4 times as many triangles are added as in the previous iteration; because the first iteration adds 3 triangles then the nth iteration will add 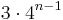 triangles. Combining these two formulae gives the iteration formula:
triangles. Combining these two formulae gives the iteration formula:
where 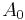 is area of the original triangle. Substituting in
is area of the original triangle. Substituting in
and expanding yields:
In the limit, as n goes to infinity, the limit of the sum of the powers of 4/9 is 4/5, so
So the area of a Koch snowflake is 8/5 of the area of the original triangle, or 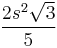 .[2] Therefore the infinite perimeter of the Koch triangle encloses a finite area.
.[2] Therefore the infinite perimeter of the Koch triangle encloses a finite area.
It is possible to tessellate the plane by copies of Koch snowflakes in two different sizes. However, such a tessellation is not possible using only snowflakes of the same size as each other. Since each Koch snowflake in the tesselation can be subdivided into seven smaller snowflakes of two different sizes, it is also possible to find tessellations that use more than two sizes at once.[3]
Thue-Morse Sequence and Turtle graphics
A Turtle Graphic is the curve that is generated if an automaton is programmed with a sequence. If the Thue–Morse sequence members are used in order to select program states:
- If t(n) = 0, move ahead by one unit,
- If t(n) = 1, rotate counterclockwise by an angle of π/3,
the resulting curve converges to the Koch snowflake.
Representation as Lindenmayer system
The Koch Curve can be expressed by a rewrite system (Lindenmayer system).
- Alphabet : F
- Constants : +, −
- Axiom : F++F++F
- Production rules:
- F → F−F++F−F
Here, F means "draw forward", + means "turn right 60°", and − means "turn left 60°".
Variants of the Koch curve
Following von Koch's concept, several variants of the Koch curve were designed, considering right angles (quadratic), other angles (Césaro) or circles and their extensions to higher dimensions (Sphereflake):
| Variant | Illustration | Construction |
|---|---|---|
| 1D, 85° angle | The Cesaro fractal is a variant of the Koch curve with an angle between 60° and 90° (here 85°). | |
| 1D, 90° angle | ||
| 1D, 90° angle | ||
| 2D, triangles | ||
| 2D, 90° angle | Extension of the quadratic type 1 curve. The illustration at left shows the fractal after the second iteration . | |
| 2D, 90° angle | Extension of the quadratic type 2 curve. The illustration at left shows the fractal after the first iteration. | |
| 2D, spheres | Eric Haines has developed the sphereflake fractal, which is a three-dimensional version of the Koch snowflake, using spheres. |
See also
- List of fractals by Hausdorff dimension
- Gabriel's Horn (infinite surface area but encloses a finite volume)
- Flowsnake
Notes and references
- ^ Addison, Paul S. Fractals and Chaos - An Illustrated Course. Institute of Physics (IoP) Publishing (1997) ISBN 0750304006 - Page 19
- ^ Koch Snowflake
- ^ Burns, Aidan (1994), "78.13 Fractal tilings", Mathematical Gazette 78 (482): 193–196, JSTOR 3618577.
- Edward Kasner & James Newman Mathematics and the Imagination Dover Press reprint of Simon & Schuster (1940) ISBN 0486417034, pp 344–51.